Baudelaire is Programmer

1.Drainage Ditches
基础的最大流问题，基本步骤是找增广路径，更新残余网络，直到搜索不到增广路径。

2.The Perfect Stall
最大二分匹配，可以使用hungary算法

bool find(int c){
    for(int j=0;j<M;j++){
        if(!graph[c][j]||inpath[j])continue;//如果没有边相连或者j被搜索过则略过
        inpath[j]=true;//把j放到增广路径上，true表示j已经被搜索过
        if(pair[j]==-1||find(pair[j])){
            pair[j]=c;//更新匹配关系
            return true;
        }
        //inpath[j]=false; 加上这句会超时，其实这里并不用回溯
        //因为inpath标识了从j出发能否找到增广路径
    }
    return false;
}
void hungary(){
    for(int i=0;i<N;i++){
        //i必定还没有被匹配
        for(int j=0;j<M;j++)inpath[j]=false;
        if(find(i))match++;
    }
}

3.Job Processing
各种借鉴。
用贪心算法分别求出A机器集合和B机器集合单阶段各自的最优解。为求得整体最优解，把A机器处理的工件的时间线和B机器处理的工件的时间线相接。
此图来自usaco官方题解：


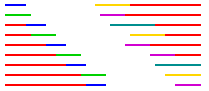
4.Cowcycles
枚举量看似很大，实际上可以水过，注意防止重复计算。
算方差可以用公式D[X]=E[X^2]-E[X]^2
枚举代码有些臃肿：

//用pick(F1,F2,R1,R2,F,R)表示在[F1,F2]区间选取F个数，在[R1,R2]区间选取R个数
void pick(int f1,int f2,int r1,int r2,int f,int r){
    int i,j;
    if(f==0&&r==0){
        calcul();
        return;
    }
    if(f*r!=0){
        for(i=f1;i<=f2-f+1;i++){
            for(j=r1;j<=r2-r+1;j++){
                seqf[F-f]=i;
                seqr[R-r]=j;
                pick(i+1,f2,j+1,r2,f-1,r-1);
            }
        }
    }
    else if(f==0){
        for(j=r1;j<=r2-r+1;j++){
            seqr[R-r]=j;
            pick(f1,f2,j+1,r2,f,r-1);
        }
    }
    else if(r==0){
        for(i=f1;i<=f2-f+1;i++){
            seqf[F-f]=i;
            pick(i+1,f2,r1,r2,f-1,r);
        }
    }
    return;
}