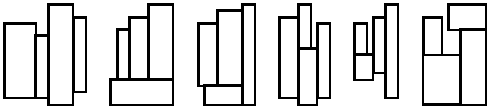
Four rectangles are given. Find the smallest enclosing (new) rectangle into which these four may be fitted without overlapping. By smallest rectangle, we mean the one with the smallest area.
All four rectangles should have their sides parallel to the corresponding sides of the enclosing rectangle. Figure 1 shows six ways to fit four rectangles together. These six are the only possible basic layouts, since any other layout can be obtained from a basic layout by rotation or reflection. Rectangles may be rotated 90 degrees during packing.
There may exist several different enclosing rectangles fulfilling the requirements, all with the same area. You must produce all such enclosing rectangles.
INPUT FORMAT
Four lines, each containing two positive space-separated integers that represent the lengths of a rectangle's two sides. Each side of a rectangle is at least 1 and at most 50.
SAMPLE INPUT (file packrec.in)
1 2 2 3 3 4 4 5
OUTPUT FORMAT
The output file contains one line more than the number of solutions. The first line contains a single integer: the minimum area of the enclosing rectangles. Each of the following lines contains one solution described by two numbers p and q with p<=q. These lines must be sorted in ascending order of p, and must all be different.
SAMPLE OUTPUT (file packrec.out)
40 4 10 5 8
这个问题给出四个矩形的边长,要求找出所有能同时包裹这四个矩形的大矩形中面积最小的那些并且按一定顺序输出,要求四个矩形要保持边之间平行放置。四个矩形的排布都可以等效为上图中六种方案之一。
方法很简单——枚举各种情况,而且稍加观察还可以发现第4和第5种放置方案是等效的。复杂的一点是第6种方案不太直观。经过一些尝试我认为可以采取以下步骤丢弃不必要的放置方式并保证结果最优: (这个方案没有经过严密的证明,是通过人肉剪枝在我脑子里形成的,只能算我的“经验步骤”。根据这个方案写的程序已经AC,不过可能有疏漏但是OJ的数据没有检测出来)
1.枚举四个位置上的矩形。
布局为:
| rc | rd |
| ra | rb |
2.仅考虑ra高度(用h(ra)表示)大于或等于rb的情况,其余情况可以简单地由此翻转得到。
我们将ra和rb紧贴并且将他们的下边沿对齐。
3.放置rc。
让rc的左边沿和ra的左边沿对齐。由于h(ra)>h(rb),rc可以伸展到rb上空。
4.放置rd。
让rd的下边沿紧贴rb并尽量向左移动。
利用此步骤,可以省略很多不必要的考虑并计算包络矩形的宽度和高度。
当然小矩形们可以90度旋转,所以要针对这一情况进行枚举。
以下是可能产生的一些特殊排布:
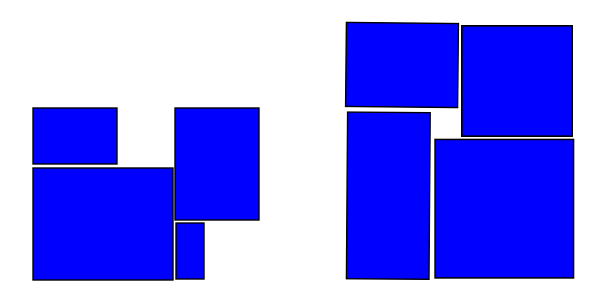
进化:
USACO给出的题解用递归的方法让代码看起来干净了很多,而且解法更具普遍性,在解决第6种布局时更是体现出了枚举方法简单粗暴的奥义:并不人为干涉矩形的拼装过程而是简单地列举出所有可能构成包络大矩形边长的几种情况并取最大的那种(请仔细瞅代码)。这看似粗暴却比我的方法高明很多,因为人为的剪枝有可能变成很耗费体力的活动。所以,这个问题教会我们:要枚举,就粗暴到底!(当然是在可接受的时间复杂度之内)
点击查看我的程序源码和USACO题解:
/*
ID: ******
LANG: C
TASK: packrec
*/
#include<stdio.h>
FILE *fin,*fout;
int minArea;
typedef struct {
int area;//面积
int p;//短边
int q;//长边
}M;//表示矩形的结构体
M memo[500];
int tailMemo;//指向memo数组最后一个记录
int rec[4][2];
int w[4];//宽度的下标用于枚举小矩形的旋转
int h[4];//高度的下标
//记录《可能》的最优方案
void testAndInsert(int rw,int rh){
int tArea = rw*rh;
if(tArea<=minArea){
minArea = tArea;
M m;
m.area = tArea;
m.p = rw<rh?rw:rh;
m.q = rw+rh-m.p;
int po = tailMemo;
if(tailMemo==-1)po=0;
else if(memo[tailMemo].area>tArea)po=tailMemo+1;
else if(memo[tailMemo].area==tArea){
if(memo[tailMemo].p>=m.p){
po=tailMemo+1;
}
int t = tailMemo;
while(memo[t].area==tArea && memo[t].p<m.p){
memo[t+1]=memo[t];
po=t;
t--;
}//这里做一个插入排序,以便按顺序输出结果
}
tailMemo++;
memo[po]=m;
}
}
int main(){
fin = fopen("packrec.in","r");
fout = fopen("packrec.out","w");
minArea = 0x7fffffff;
tailMemo = -1;
int i;
for(i=0;i<4;i++)fscanf(fin,"%d %d",&rec[i][0],&rec[i][1]);
for(w[0]=0;w[0]<=1;w[0]++)
for(w[1]=0;w[1]<=1;w[1]++)
for(w[2]=0;w[2]<=1;w[2]++)
for(w[3]=0;w[3]<=1;w[3]++){//枚举矩形的旋转
int j;
for(j=0;j<4;j++)h[j]=1-w[j];
int rw,rh;
//layout 1
rw = 0;
for(j=0;j<4;j++)rw+=rec[j][w[j]];
rh = rec[0][h[0]];
for(j=1;j<4;j++)rh = rec[j][h[j]]>rh?rec[j][h[j]]:rh;
testAndInsert(rw,rh);
//layout 2
for(j=0;j<4;j++){
rw = rec[j][w[j]];
int tw = 0;
rh = 0;
int k;
for(k=0;k<4;k++){
if(k!=j){
tw+=rec[k][w[k]];
rh =rec[k][h[k]]>rh?rec[k][h[k]]:rh;
}
}
rw = tw>rw?tw:rw;
rh+=rec[j][h[j]];
testAndInsert(rw,rh);
}
//layout 3 4 5
int ra,rb;
for(ra=0;ra<4;ra++)
for(rb=0;rb<4;rb++){
if(rb==ra)continue;
//3
rw=rec[ra][w[ra]];
rh=rec[rb][h[rb]];
int th=0;
int tw=0;
for(j=0;j<4;j++)if(j!=ra&&j!=rb){
tw+=rec[j][w[j]];
th=rec[j][h[j]]>th?rec[j][h[j]]:th;
}
th+=rec[ra][h[ra]];
rh=rh>th?rh:th;
rw=rw>tw?rw:tw;
rw+=rec[rb][w[rb]];
testAndInsert(rw,rh);
//4 5
int rw1,rh1;
rh1=rec[ra][h[ra]]+rec[rb][h[rb]];
rw1=rec[ra][w[ra]]>rec[rb][w[rb]]?rec[ra][w[ra]]:rec[rb][w[rb]];
for(j=0;j<4;j++)if(j!=ra&&j!=rb){
rw1+=rec[j][w[j]];
rh1=rh1>rec[j][h[j]]?rh1:rec[j][h[j]];
}
testAndInsert(rw1,rh1);
}
//layout 6
int rc,rd;
for(ra=0;ra<4;ra++)
for(rb=0;rb<4;rb++){
if(rb==ra)continue;
for(rc=0;rc<4;rc++){
if(rc==ra||rc==rb)continue;
for(rd=0;rd<4;rd++){
if(rd==ra||rd==rb||rd==rc)continue;
if(rec[ra][h[ra]]>=rec[rb][h[rb]]){
rw=rec[ra][w[ra]]+rec[rb][w[rb]];
int tw=rec[ra][w[ra]]>rec[rc][w[rc]]?rec[ra][w[ra]]:rec[rc][w[rc]];
tw+=rec[rd][w[rd]];
if(rw<tw)rw=tw;
rh=rec[ra][h[ra]]+rec[rc][h[rc]];
int th=rec[rb][h[rb]]+rec[rd][h[rd]];
rh=rh>th?rh:th;
testAndInsert(rw,rh);
}
}
}
}
}
int prep=0;
int po=tailMemo;
fprintf(fout,"%d\n",minArea);
while(po>=0&&memo[po].area==minArea){
if(memo[po].p==prep){
po--;
continue;
}
prep=memo[po].p;
fprintf(fout,"%d %d\n",memo[po].p,memo[po].q);
po--;
}
return 0;
}
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
typedef struct Rect Rect;
struct Rect {
int wid;
int ht;
};
Rect
rotate(Rect r)
{
Rect nr;
nr.wid = r.ht;
nr.ht = r.wid;
return nr;
}
int
max(int a, int b)
{
return a > b ? a : b;
}
int
min(int a, int b)
{
return a < b ? a : b;
}
int tot;
int bestarea;
int bestht[101];
void
record(Rect r)
{
int i;
if(r.wid*r.ht < tot)
*(long*)0=0;
if(r.wid*r.ht < bestarea || bestarea == 0) {
bestarea = r.wid*r.ht;
for(i=0; i<=100; i++)
bestht[i] = 0;
}
if(r.wid*r.ht == bestarea)
bestht[min(r.wid, r.ht)] = 1;
}
void
check(Rect *r)
{
Rect big;
int i;
/* schema 1: all lined up next to each other */
big.wid = 0;
big.ht = 0;
for(i=0; i<4; i++) {
big.wid += r[i].wid;
big.ht = max(big.ht, r[i].ht);
}
record(big);
/* schema 2: first three lined up, fourth on bottom */
big.wid = 0;
big.ht = 0;
for(i=0; i<3; i++) {
big.wid += r[i].wid;
big.ht = max(big.ht, r[i].ht);
}
big.ht += r[3].ht;
big.wid = max(big.wid, r[3].wid);
record(big);
/* schema 3: first two lined up, third under them, fourth to side */
big.wid = r[0].wid + r[1].wid;
big.ht = max(r[0].ht, r[1].ht);
big.ht += r[2].ht;
big.wid = max(big.wid, r[2].wid);
big.wid += r[3].wid;
big.ht = max(big.ht, r[3].ht);
record(big);
/* schema 4, 5: first two rectangles lined up, next two stacked */
big.wid = r[0].wid + r[1].wid;
big.ht = max(r[0].ht, r[1].ht);
big.wid += max(r[2].wid, r[3].wid);
big.ht = max(big.ht, r[2].ht+r[3].ht);
record(big);
/*
* schema 6: first two pressed next to each other, next two on top, like:
* 2 3
* 0 1
*/
big.ht = max(r[0].ht+r[2].ht, r[1].ht+r[3].ht);
big.wid = r[0].wid + r[1].wid;
/* do 2 and 1 touch? */
if(r[0].ht < r[1].ht)
big.wid = max(big.wid, r[2].wid+r[1].wid);
/* do 2 and 3 touch? */
if(r[0].ht+r[2].ht > r[1].ht)
big.wid = max(big.wid, r[2].wid+r[3].wid);
/* do 0 and 3 touch? */
if(r[1].ht < r[0].ht)
big.wid = max(big.wid, r[0].wid+r[3].wid);
/* maybe 2 or 3 sits by itself */
big.wid = max(big.wid, r[2].wid);
big.wid = max(big.wid, r[3].wid);
record(big);
}
void
checkrotate(Rect *r, int n)
{
if(n == 4) {
check(r);
return;
}
checkrotate(r, n+1);
r[n] = rotate(r[n]);
checkrotate(r, n+1);
r[n] = rotate(r[n]);
}
void
checkpermute(Rect *r, int n)
{
Rect t;
int i;
if(n == 4)
checkrotate(r, 0);
for(i=n; i<4; i++) {
t = r[n], r[n] = r[i], r[i] = t; /* swap r[i], r[n] */
checkpermute(r, n+1);
t = r[n], r[n] = r[i], r[i] = t; /* swap r[i], r[n] */
}
}
void
main(void)
{
FILE *fin, *fout;
Rect r[4];
int i;
fin = fopen("packrec.in", "r");
fout = fopen("packrec.out", "w");
assert(fin != NULL && fout != NULL);
for(i=0; i<4; i++)
fscanf(fin, "%d %d", &r[i].wid, &r[i].ht);
tot=(r[0].wid*r[0].ht+r[1].wid*r[1].ht+r[2].wid*r[2].ht+r[3].wid*r[3].ht);
checkpermute(r, 0);
fprintf(fout, "%d\n", bestarea);
for(i=0; i<=100; i++)
if(bestht[i])
fprintf(fout, "%d %d\n", i, bestarea/i);
exit(0);
}
